|
|
|
Astral Imaging at Dogwood Ridge Observatory |
Latitude: 37°48'51.0" N" |
|
|
|
|
|
|
|||
 |
|
|
|
||
|
|
|
|
|||
|
(click on thumbnails to go to that image's page)
|
|||||
| ||||||||||||||||||||||||
|
|
Pix Insight As you see I have also defined an uniform RGB working space (same luminance weights for red, green and blue). This won't confer more relevance to any specific color to compute the luminance. As the image has a variety of emission and reflexion nebulae, this choice seems reasonable. The second step is building a star mask, which we'll use later as a deringing support to protect the brightest stars during deconvolution. Note that we only want to protect just the brightest stars; Deconvolution's global deringing is very efficient to protect the rest of small-scale, high-contrast objects. In this case, I've just applied the StarMask tool with default parameters, as shown in the next screenshot. Now let's start deconvolving the image. As always, the ScreenTransferFunction tool must be used to make the linear image visible without altering it. I've just applied the Auto Stretch feature. This is a deconvolved preview shown at 3:1 magnification: 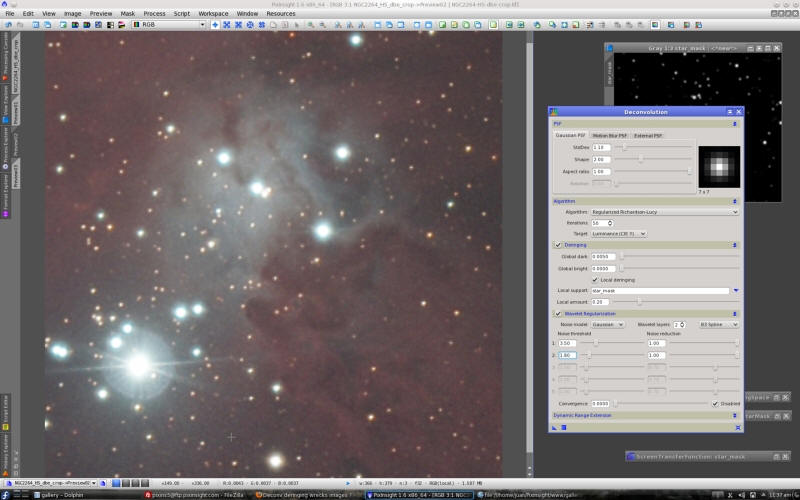 Your image does not have very high SNR, so the benefits of deconvolution cannot be spectacular. However, the achieved star reduction and the nice sharpening effect on the nebulas, especially on dark structures, are well worth the effort in my opinion. The standard deviation of the Gaussian PSF is 1.1 pixels. I have derived this value from measuring the smallest stars in your image, and after some experimentation. I think it is very close to the true PSF in your image (I haven't measured it; this is a quick test). Now let's see what happens if we disable some features of the deconvolution algorithm. This is the best way to understand how they work. First we'll disable wavelet noise regularization: Pretty ugly, isn't it? Regularization works by applying a wavelet-based noise analysis and reduction routine in tandem with deconvolution, at each iteration. It is very efficient, as you can see by comparing the previous two screenshots. In fact, our implementation of wavelet regularized deconvolution easily outperforms other implementations, including the classical Richardson-Lucy and Van Cittert algorithms, as well as Maximum Entropy. The original regularization algorithms have been created by Jean-Luc Starck and Fionn Murtagh (http://www.multiresolution.com/cupbook.html). I have slightly modified and adapted them to our working tools. Our implementation has the advantage that you can fine tune regularization parameters very easily. Let's continue with our 'disabling things tour'. Now we'll re-enable regularization but disable deringing: Actually not less ugly than before  This is the Gibbs phenomenon in all its splendor!
This is the Gibbs phenomenon in all its splendor!We have two deringing algorithms implemented in our Deconvolution tool: local and global deringing. Global deringing, as its name suggests, is applied equally to the whole image. This is an incredibly efficient algorithm created by Vicent Peris; all of us should be grateful to him for having devised such a nice thing. In many cases global deringing is sufficient. However, when there are bright stars and other large and very bright features, we often need an increased level of protection. This happens because large stars cannot be deconvolved in the same way as the rest of the image. We address this problem with the local deringing algorithm. Local deringing is driven by a special image (usually a star mask) that is used to change the way deconvolution works at each iteration: the local deringing support. Local deringing support images are very easy to build: it usually suffices with a relatively rough star mask covering the brightest objects. With the combination of local and global deringing, we can manage virtually any ringing problem in deconvolution. To better illustrate how both deringing algorithms work, we'll see what happens if we disable local deringing in this case: Note the ringing problems that persist around the brightest stars. Finally, let's re-enable everyting. This is the result of Deconvolution with regularization and local+global deringing for the same preview: And for further comparison, this is the same preview from the original image, before deconvolution: 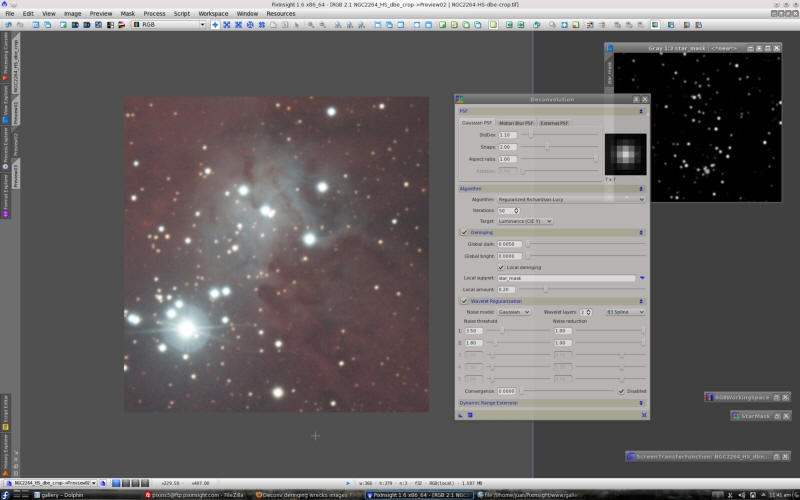 I think that even if your image doesn't have a very high SNR, deconvolution with the appropriate control features provides a very nice result.
|
| |||||||||||||||||||||||||||||